Задача
Длина каждой стороны выпуклого четырёхугольника ABCD не меньше 1 и не больше 2. Его диагонали пересекаются в точке O.
Докажите, что SAOB + SCOD ≤ 2(SAOD + SBOC).
Решение
Достаточно доказать, что одно из отношений AO/OC и BO/OD не меньше ½ и не больше 2. Действительно, если, скажем, отношение AO/OC такое, то
SA0B ≤ 2SBOC и SCOD ≤ 2SAOD, откуда и следует требуемое.
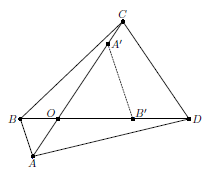
Без ограничения общности можно считать, что AO ≤ OC, BO ≤ OD. Предположим противное: пусть AO ≤ ½ OC, BO ≤ ½ OD. Отложим на отрезках OC, OD соответственно отрезки OA' = 2OA, OB' = 2OB (см. рис.). Тогда A'B' = 2AB ≥ 2, и точки A', B' лежат на сторонах треугольника COD (не совпадая с вершинами). Значит, отрезок A'B' меньше одной из сторон этого треугольника (см. задачу 155155). Оценим стороны треугольника COD.
По условию CD ≤ 2. Поскольку точка O лежит между B и D, то отрезок CO не больше одной из сторон CB и CD, следовательно, CD ≤ 2 и аналогично
DO ≤ 2. Отрезок A'B' должен быть меньше одной из этих сторон, но A'B' ≥ 2. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь