Назад
Задача 164392 • Сложность: 3 • 8-9 класс
Задача

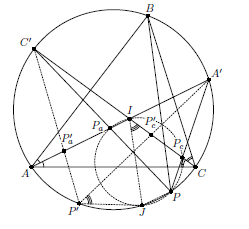
Пусть P – произвольная точка на дуге AC описанной окружности треугольника ABC, не содержащей точки B. Биссектриса угла APB пересекает биссектрису угла BAC в точке Pa; биссектриса угла CPB пересекает биссектрису угла BCA в точке Pc. Докажите, что для всех точек P центры описанных окружностей треугольников PPaPc лежат на одной прямой.

Авторы:
Дмитриев И.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина IX Олимпиада по геометрии имени И.Ф. Шарыгина (2013 г.)
Количество версий:
3
Решение

  Прямые PPa, PPc вторично пересекают описанную окружность треугольника в серединах C', A' дуг AB, BC (см. рис.).

  Поэтому  ∠PaPPc= ½ (∠A+ ∠C) = 180° – ∠AIC,  гдеI– центр вписанной окружности треугольника. Значит, окружностьPPaPcпроходит через точкуI. Зафиксируем теперь какое-нибудь положение точкиPи вторую точкуJпересечения описанных окружностей треугольниковPPaPcиABC. Для любой другой точкиP'имеем  ∠JP'P'c= ∠JP'A'= 180° – ∠JPA'= 180° – ∠JPPc= ∠JIPc= ∠JIP'c  (еслиPиP'расположены, как на рисунке, в других случаях рассуждения аналогичны), то есть окружностьP'P'aP'cтакже проходит черезJ. Следовательно, центры всех окружностейPPaPcлежат на серединном перпендикуляре к отрезкуIJ.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет