Задача
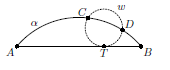
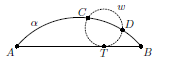
На отрезке AB построена дуга α (см. рис.). Окружность ω касается отрезка AB в точке T и пересекает α в точках C и D. Лучи AC и TD пересекаются в точке E, лучи BD и TC – в точке F. Докажите, что прямые EF и AB параллельны.
Решение
Поскольку AB – касательная к окружности ω, то ∠TCD = ∠BTD. Поэтому
∠FCE = ∠ACT = ∠ACD – ∠TCD = (180° – ∠ABD) – ∠BTD = ∠TDB = ∠FDE. Следовательно, CDEF – вписанный четырёхугольник.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет