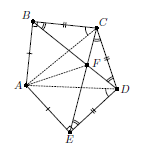
Решение 1:   Из условия задачи следует, что прямоугольные треугольники ABC и AED равны, то есть треугольник ACD – равнобедренный (см. рис.).

  Тогда  ∠BCD= ∠BCA+ ∠ACD= ∠EDA+ ∠ADC= ∠CDE.  Следовательно, равнобедренные треугольникиBCDиCDEравны. Таким образом, ∠CBD= ∠CDB= ∠ECD= ∠DEC.   Из того, что треугольникCFD– равнобедренный, и из равенства отрезковBDиCEследует, что  BF = FE.  Следовательно, треугольникиABFиAEFравны. Тогда ∠ABF= ½ ∠BFE= ½ (180° – 2∠FCD) = 90° – ∠ECD= 90° – ∠DBC= ∠ABF, откуда  AB = AF.

Решение 2:   Пусть BC пересекает DE в точке P (см. рис.).

  ТреугольникABE– равнобедренный, следовательно,  ∠ABE= ∠AEB.  Тогда в четырёхугольникеBCDEравны стороныBCиDEи углыCBEиDBE, поэтому этот четырёхугольник – равнобокая трапеция. Следовательно,  ∠CBD= ∠CDB= ∠DBE,  то естьBD– биссектриса углаCBE. Значит,F– центр вписанной окружности треугольникаPBE. Из симметрии и вписанности четырёхугольникаPBAEследует, что точкаA– середина дугиBEописанной окружности треугольникаPBE, а, значит, полемме о трезубце(см. задачу153119) AF = AB.

Ответ задачи отсутствует