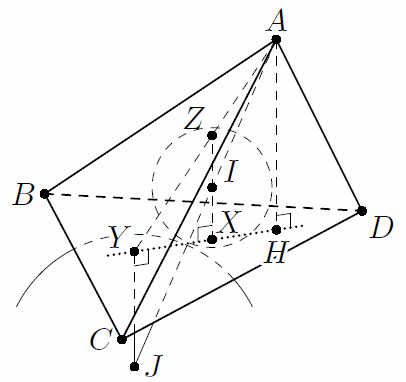
Первый способ. Пусть гомотетия с центром в точке A, переводящая вневписанную сферу во вписанную, переводит точку Y в некоторую точку Z вписанной сферы. Эта гомотетия переводит плоскость (BCD) в плоскость, параллельную (BCD) и касающуюся вписанной сферы в точке Z. Значит, X и Z – диаметрально противоположные точки вписанной сферы, а следовательно,  XZ ⊥ (BCD).  Поскольку Z лежит на отрезке AY, то  ∠AXY > ∠ZXY = 90°

Второй способ. Пусть I и J – соответственно центры вписанной и вневписанной сфер, а AH – высота пирамиды. Точки A, I и J лежат на одной прямой (все точки которой равноудалены от плоскостей (ABC), (ACD) и (ADB)), причём I лежит между A и J. Значит, их проекции H, X и Y на плоскость (BCD) также лежат на одной прямой, причём X лежит между H и Y. Итак, основание высоты AH треугольника AXY лежит вне стороны XY, и, следовательно, этот треугольник – тупоугольный.

Ответ задачи отсутствует