Задача
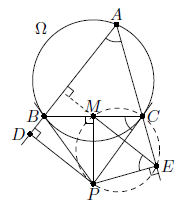
Остроугольный треугольник ABC вписан в окружность Ω. Касательные, проведённые к Ω в точках B и C, пересекаются в точке P. Точки D и E – основания перпендикуляров, опущенных из точки P на прямые AB и AC. Докажите, что точка пересечения высот треугольника ADE является серединой отрезка BC.
Решение
Пусть M – середина BC. Треугольник BPC равнобедренный, значит, его медиана PM является высотой. Поэтому четырёхугольник MCEP вписан в окружность с диаметром CP. Следовательно, ∠MEP = ∠MCP = ∠BAC и ∠MEA + ∠BAC = (90° – ∠MEP) + ∠BAC = 90°, откуда ME ⊥ AB (см. рис.). Аналогично MD ⊥ AC. Это и значит, что M – точка пересечения высот треугольника ADE.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет