Задача
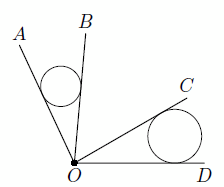
Внутри угла AOD проведены лучи OB и OC, причём ∠AOB = ∠COD. В углы AOB и COD вписаны непересекающиеся окружности.
Докажите, что точка пересечения общих внутренних касательных к этим окружностям лежит на биссектрисе угла AOD.
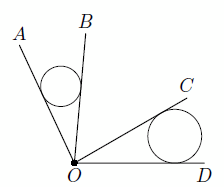
Решение
Пусть O1 и O2 – центры данных окружностей, R1 и R2 – их радиусы, L – точка пересечения касательных. Заметим, что окружности гомотетичны с центром L, то есть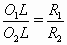 
. С другой стороны, из подобия прямоугольных треугольников с гипотенузами OO1 и OO2 (см. рис.) следует, что 
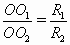. Таким образом, 
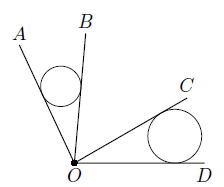, откуда следует, что OL – биссектриса треугольника O1OO2, а значит, и угла AOD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет