Пусть I – центр вписанной окружности треугольника ABC (см. рис.). Докажем, что описанная окружность треугольника ABI проходит через точку A₁.

  Первый способ.  ∠AIB = 90° + ½ ∠C  (см. задачу 155448), а  ∠CA₁A = ∠CAA₁ = 90° – ½ ∠C = 180° – ∠AIB.    Второй способ. Центр описанной окружности треугольника Ω треугольника AIB совпадает с серединой дуги AB описанной окружности треугольника ABC ("теорема о трилистнике", см. задачу 153119). Следовательно, окружность Ω пересекает сторону CB в точке, симметричной точке A, то есть в A₁.

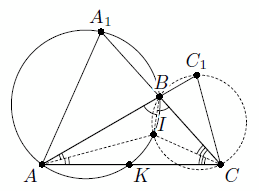
  Аналогично, описанная окружность треугольника СIB проходит через точку C₁. Следовательно, описанные окружности треугольников ABA₁ и CBC₁ пересекаются в точке I.

Ответ задачи отсутствует