Задачи и олимпиады по математике

Задача

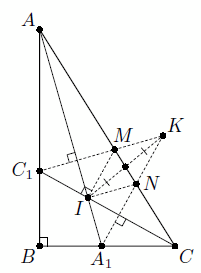
Биссектрисы AA₁ и CC₁ прямоугольного треугольника ABC (∠B = 90°) пересекаются в точке I. Прямая, проходящая через точку C₁ и перпендикулярная прямой AA₁, пересекает прямую, проходящую через A₁ и перпендикулярную CC₁, в точке K. Докажите, что середина отрезка KI лежит на отрезке AC.

Решение

Пусть данные прямые пересекают сторону AC в точках M и N соответственно (см. рис.).

Заметим, что треугольник C₁AM – равнобедренный (биссектриса совпадает с высотой). Тогда треугольник C₁IM – также равнобедренный (C₁I = MI). Но ∠AIC₁ = 180° – ∠AIC = 45° (см. задачу 155448), то есть ∠CIM = 90°. Следовательно, прямые MI и KA₁ параллельны. Аналогично NI || C₁K, то есть MINK – параллелограмм, и его диагонали делятся точкой пересечения пополам.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления