Задача
В треугольнике ABC биссектриса AK перпендикулярна медиане CL.
Докажите, что в треугольнике BKL также одна из биссектрис перпендикулярна одной из медиан.
Решение
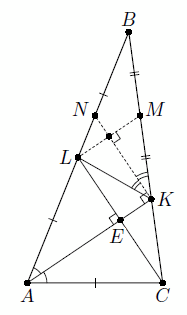
Докажем, что биссектриса KN и медиана LM треугольника BKL перпендикулярны (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет