Задачи и олимпиады по математике

Задача

Касательные к параболе в точках$\alpha$,$\beta$,$\gamma$образуют треугольникABC(рис.). Докажите, что: а) описанная окружность треугольника ABC проходит через фокус параболы; б) высоты треугольника ABC пересекаются в точке, лежащей на директрисе параболы; в)$S_{\alpha\beta\gamma}=2S_{ABC}$; г)$\sqrt[3]{S_{\alpha\beta C}}+\sqrt[3]{S_{\beta\gamma A}}= \sqrt[3]{S_{\alpha\gamma B}}$.

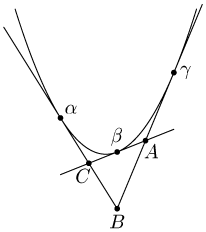
Решение

а) Проекция фокусаFна касательную к параболе лежит на касательной к параболе, перпендикулярной оси. Поэтому проекцииA',B',C'фокусаFна прямыеBC,CA,ABлежат на одной прямой. Это означает, что точкаFлежит на описанной окружности треугольникаABC. В самом деле,$\angle$AFC'=$\angle$AB'C'=$\angle$A'B'C=$\angle$A'FC, поэтому$\angle$CFA=$\angle$A'FC'= 180^o-$\angle$B. б) Касательные к параболеx²= 4yв точках(2t_i,t_i²) задаются уравнениямиy=t_ix-t_i². Они пересекаются в точках(t_i+t_j,t_it_j). Легко проверить, что ортоцентром треугольника с вершинами в трех таких точках служит точка(t₁+t₂+t₃+t₁t₂t₃, - 1). в) Можно считать, что парабола задается уравнениемx²= 4y. В таком случае точки$\alpha$,$\beta$,$\gamma$имеют координаты(2t_i,t_i²),i= 1, 2, 3. Легко проверить, что

S_{$\scriptstyle \alpha$$\scriptstyle \beta$$\scriptstyle \gamma$} = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \begin{vmatrix} 2t_1&t^2_1&1 \\ 2t_2&t^2_2&1 \\ 2t_3&t_3^2&1 \end{vmatrix}$, S_ABC = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \begin{vmatrix} t_2+t_3&t_2t_3&1 \\ t_3+t_1&t_3t_1&1 \\ t_1+t_2&t_1t_2&1 \end{vmatrix}$.

г) Существует аффинное преобразование, переводящее ось параболы и прямуюACв пару перпендикулярных прямых. Поэтому можно считать, что точки$\alpha$,$\beta$,$\gamma$имеют координаты(2t₁,t₁²),(0, 0),(2t₃,t₃²), причемt₁< 0 иt₃> 0. В таком случае

S_{$\scriptstyle \alpha$$\scriptstyle \beta$C} = - $\displaystyle {\textstyle\frac{1}{2}}$t₁³, S_{$\scriptstyle \beta$$\scriptstyle \gamma$A} = $\displaystyle {\textstyle\frac{1}{2}}$t₃³, S_{$\scriptstyle \alpha$$\scriptstyle \beta$B} = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \begin{vmatrix} 2t_3&t_3^2&1 \\ 2t_1&t_1^2&1 \\ t_1+t_3&t_1t_3&1 \end{vmatrix}$ = $\displaystyle {\frac{(t_3-t_1)^3}{2}}$.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления