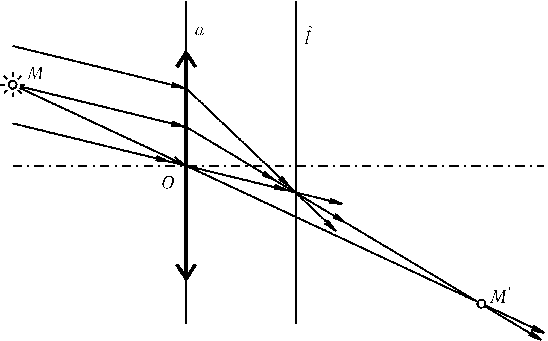
Пусть O — центр линзы,$\pi$ — некоторая плоскость, проходящая через ее оптическую ось aи f — прямые пересечения плоскости $\pi$с плоскостью линзы и с фокальной плоскостью соответственно (a|f). В школьном курсе физики показано, что если пренебречь толщиной линзы, то изображение M'точки M, лежащей в плоскости $\pi$, строится следующим образом (рис.). Проведем через точку Mпроизвольную прямую l; пусть A — точка пересечения прямых aи l,B — точка пересечения прямой fс прямой, проходящей через Oпараллельно l. Тогда M'есть точка пересечения прямыхABи OM. Докажите, что преобразование плоскости $\pi$, сопоставляющее каждой точке ее изображение, является проективным. Таким образом, через увеличительное стекло мы видим образ нашего мира при проективном преобразовании.