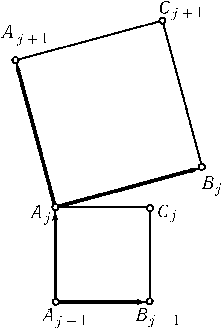
Установим соответствие между точками плоскости и комплексными числами так, чтобы точкаOсовпала с нулем. ТогдаB_j-A_j= -i(A_{j + 1}-A_j) иC_j-A_j= -i(A_j-A_{j - 1}) (см. рис.; мы считаем, чтоA₀=A_nиA_{n + 1}=A₁). Вычитая второе равенство из первого, получаемB_j-C_j= -i(A_{j - 1}+A_{j + 1}- 2A_j). Но согласно задаче 29.8.1A_{j - 1}+A_{j + 1}= 2 cos(2$\pi$/n)A_j. Значит,B_j-C_j= 2i$\bigl($1 - cos(2$\pi$/n)$\bigr)$A_j.

Ответ задачи отсутствует