Задачи и олимпиады по математике

Задача

Пусть точкиA,B,C,Dявляются образами точекA,B,C,Dпри инверсии. Докажите, что: а)${\frac{AC}{AD}}$:${\frac{BC}{BD}}$=${\frac{A^C^}{A^D^}}$:${\frac{B^C^}{B^D^}}$; б)$\angle$(DA,AC) -$\angle$(DB,BC) =$\angle$(DB,BC) -$\angle$(DA,AC).

Решение

Установим соответствие между точками плоскости и комплексными числами так, чтобы центр инверсии находился в нуле. Тогда образом числаzпри инверсии со степеньюRявляется числоR/$\bar{z}$.Двойным отношениемкомплексных чиселa,b,c,dназывают комплексное число

(abcd )= $\displaystyle {\frac{a-c}{a-d}}$ : $\displaystyle {\frac{b-c}{b-d}}$.

Еслиa^*,b^*,c^*,d^* — образы чиселa,b,c,dпри инверсии, то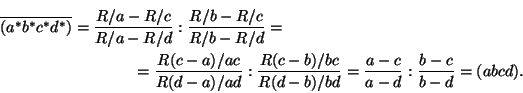

$\begin{multline*} \overline{(a^*b^*c^*d^*)}= \frac{R/a-R/c}{R/a-R/d}:\frac{R/b... ...R(c-b)/bc}{R(d-b)/bd}= \frac{a-c}{a-d}:\frac{b-c}{b-d}=(abcd). \end{multline*}$

Задача а) следует из равенства модулей этих чисел, а задача б) — из равенства их аргументов.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления