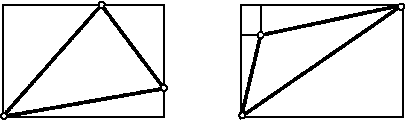
Пусть a₁и a₂ — какие-нибудь две перпендикулярные прямые. Поскольку аффинное преобразование сохраняет отношение длин параллельных отрезков, то длины всех отрезков, параллельных одной прямой, умножаются на один и тот же коэффициент. Обозначим через k₁и k₂эти коэффициенты для прямых a₁и a₂. Пусть $\varphi$ — угол между образами этих прямых. Докажем, что данное аффинное преобразование изменяет площади всех многоугольников в kраз, гдеk=k₁k₂sin$\varphi$. Для прямоугольника со сторонами, параллельными a₁и a₂, а также для прямоугольного треугольника с катетами, параллельными a₁и a₂, это утверждение очевидно. Любой другой треугольник можно получить, отрезав от прямоугольника со сторонами, параллельными a₁и a₂, несколько прямоугольных треугольников с катетами, параллельными a₁и a₂(рис.), и, наконец, согласно задаче 22.22, любой многоугольник можно разрезать на треугольники.

Ответ задачи отсутствует