Задача
На плоскости дан многоугольникA1A2...Anи точкаOвнутри его. Докажите, что равенства
| $\displaystyle \overrightarrow{OA_1}$ + $\displaystyle \overrightarrow{OA_3}$ = 2 cos$\displaystyle {\frac{2\pi}{n}}$$\displaystyle \overrightarrow{OA_2}$, | |
| 1$\displaystyle \overrightarrow{OA_2}$ + $\displaystyle \overrightarrow{OA_4}$ = 2 cos$\displaystyle {\frac{2\pi}{n}}$$\displaystyle \overrightarrow{OA_3}$, | |
| to4.5cm $\displaystyle \dotfill$ | |
| $\displaystyle \overrightarrow{OA_{n-1}}$ + $\displaystyle \overrightarrow{OA_1}$ = 2 cos$\displaystyle {\frac{2\pi}{n}}$$\displaystyle \overrightarrow{OA_n}$. |
необходимы и достаточны для того, чтобы существовало аффинное преобразование, переводящее данный многоугольник в правильный, а точкуO — в его центр.
Решение
Докажем сначала, что еслиA1A2...An — правильный многоугольник, вписанный в единичную окружность, аO — его центр, то указанные в условии задачи равенства выполняются, т. е.
$\displaystyle \overrightarrow{OA_{i-1}}$ + $\displaystyle \overrightarrow{OA_{i+1}}$ = 2k$\displaystyle \overrightarrow{OA_i}$, i = 1,..., n1)
(мы считаем, чтоA0=AnиAn + 1=A1; черезkобозначено числоcos(2$\pi$/n)). Для этого при каждом фиксированномiвыберем на плоскости
систему координат с центром в точкеOи осьюOx, направленной вдоль лучаOAi. Тогда точкиAi - 1,AiиAi + 1имеют координаты$\bigl($k, - sin(2$\pi$/n)$\bigr)$, (1, 0) и$\bigl($k, sin(2$\pi$/n)$\bigr)$соответственно. Равенство (1) при данномiтеперь легко проверяется.
В силу задачи29.4равенства (1) выполняются также для образа правильногоn-угольника при аффинном преобразовании.
Наоборот, пусть для многоугольникаA1A2...Anи точкиOвнутри его
выполнены равенства (1). Возьмем правильный многоугольникB1B2...Bnс
центромOи рассмотрим аффинное преобразованиеL, которое переводит
треугольникOB1B2в треугольникOA1A2. Докажем индукцией поi, чтоL(Bi) =Aiдля всехi$\ge$2. Приi= 2 это утверждение следует из
определения отображенияL. Предположим, что мы его доказали для всех чисел,
не превосходящихi, и докажем дляi+ 1. Так как для правильных
многоугольников равенства (1) уже доказаны, а для многоугольникаA1A2...Anони выполнены по предположению, то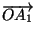
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет