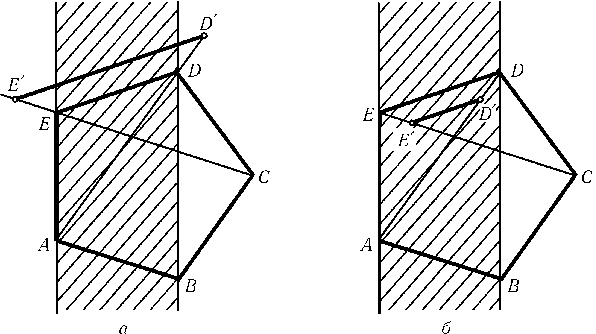
ПустьABCDE — правильный пятиугольник. Согласно задаче29.6, б) существует аффинное преобразование, которое три последовательные вершины данного пятиугольника переводит в точкиA,B,C. ПустьD'иE' — образы остальных двух вершин при этом преобразовании. Докажем, что они совпадают сDиE. С одной стороны,AD'|BCиCE'|AB, поэтому точкаD'лежит на прямойAD, а точкаE' — на прямойCE. С другой стороны,E'D'|AC|ED, поэтому если бы точкиD'иE'не совпадали с точкамиDиE, то либо они обе были бы вне полосы, ограниченной прямымиAEиBD(рис., а), либо обе внутри этой полосы (рис., б). В обоих случаях прямыеAE'иBD'не были бы параллельны.

Ответ задачи отсутствует