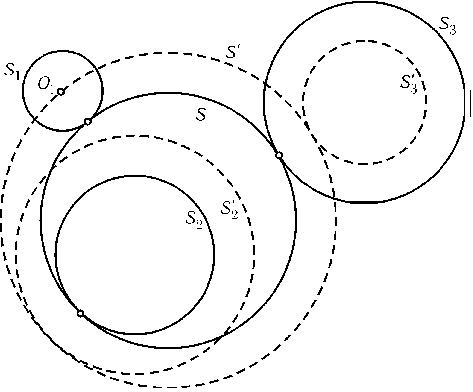
Сведем эту задачу к задаче 28.10. Пусть окружность Sрадиуса rкасается окружностей S₁,S₂,S₃радиусов r₁,r₂,r₃соответственно. Касание окружности Sс каждой из S_i(i= 1, 2, 3) может быть как внешним, так и внутренним, поэтому всего возможно восемь различных случаев касания. Пусть, например,Sкасается S₁и S₃внешним, а S₂ — внутренним образом (рис.). Заменим окружности S,S₂,S₃на концентрические им окружности S',S₂',S₃' так, чтобы S'касалась S₂' и S₃' и проходила через центр O₁окружности S₁. Для этого достаточно, чтобы радиусы S',S₂',S₃' равнялисьr+r₁,r₂+r₁, |r₃-r₁|. Обратно, по окружности S', проходящей через O₁и касающейся S₂' и S₃' (внешне, еслиr₃-r₁$\ge$0, и внутренне, еслиr₃-r₁< 0), мы можем построить окружность S, дающую решение задачи, уменьшив радиус S'на r₁. Построение такой окружности S'описано в решении задачи 28.10(если виды касания заданы, то окружность строится однозначно). Таким же способом можно выполнить построение и в остальных возможных вариантах касания.

Ответ задачи отсутствует