Дляn= 3 и n= 6 утверждение вытекает из предыдущей задачи, поэтому будем в дальнейшем считать, чтоn ≠ 3, 4, 6. Предположим, что существуют правильныеn-угольники с вершинами в узлах целочисленной решетки(n ≠ 3, 4, 6). Среди всех такихn-угольников можно выбрать тот, у которого длина стороны наименьшая. (Для доказательства достаточно заметить, что если a — длина отрезка с концами в узлах решетки, тоa=$\sqrt{n^2+m^2}$, где nи m — целые числа, поэтому длина отрезка с концами в узлах решетки может принимать лишь конечное число различных значений, меньших данного.) Пусть$\overrightarrow{A_iB_i}$=$\overrightarrow{A_{i+1}A_{i+2}}$. ТогдаB₁...B_n — правильныйn-угольник, вершины которого лежат в узлах целочисленной решетки, а его сторона меньше стороныn-угольникаA₁...A_n. Дляn= 5 и дляn$\ge$7 это видно из рисунков. Получено противоречие с выборомn-угольника

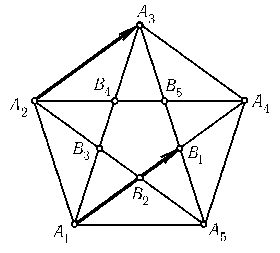
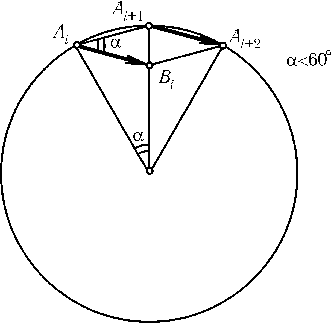
Ответ задачи отсутствует