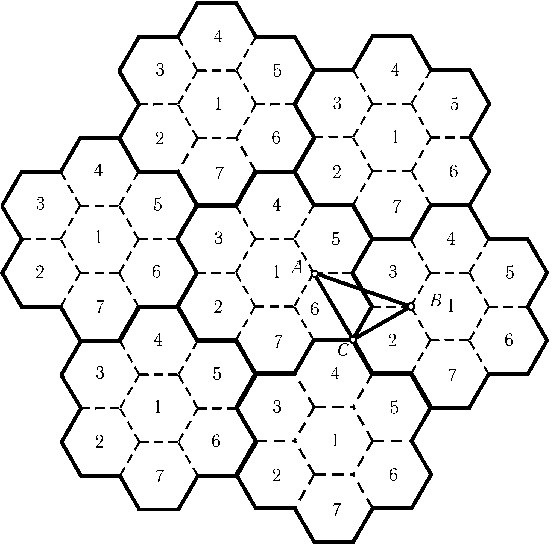
Приведем пример раскраски плоскости в семь цветов, для которой расстояние между любыми двумя одноцветными точками не равно 1. Разобьем плоскость на равные шестиугольники со стороной aи окрасим их, как показано на рис. (точки, принадлежащие двум или трем шестиугольникам, можно красить в любой из цветов этих шестиугольников). Наибольшее расстояние между точками одного цвета, лежащими в одном шестиугольнике, не превосходит 2a, а наименьшее расстояние между точками одного цвета, лежащими в разных шестиугольниках, не меньше длины отрезкаAB(см. рис.). Ясно, чтоAB²=AC²+BC²= 4a²+ 3a²= 7a²> (2a)². Поэтому, если2a< 1 <$\sqrt{7}$a, т. е.1/$\sqrt{7}$<a< 1/2, то расстояние между точками одного цвета не может быть равно 1.

Ответ задачи отсутствует