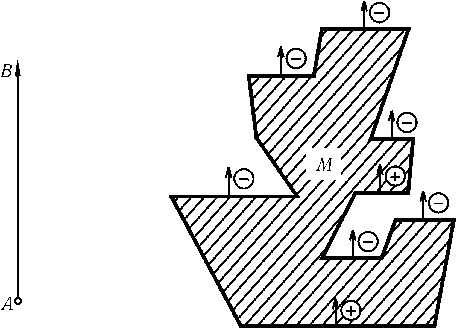
Фиксируем на плоскости некоторый лучAB. Любому многоугольнику Mпоставим в соответствие числоF(M) (зависящее отAB) следующим образом. Рассмотрим все стороны M, перпендикулярныеAB, и каждой из них поставим в соответствие число ±l, где l — длина этой стороны и знак к плюск берется, если мы, идя от этой стороны в направлении лучаAB, попадаем внутрь M, а знак к минуск — если наружу (рис.). Сумму всех полученных чисел мы и обозначимF(M); если у Mнет сторон, перпендикулярныхAB, тоF(M) = 0.

Легко видеть, что если многоугольник Mразрезан на многоугольники M₁и M₂, тоF(M) =F(M₁) +F(M₂), а если M'получен из Mпараллельным переносом, тоF(M') =F(M). Поэтому, если M₁и M₂можно разрезать на части, переводящиеся друг в друга параллельным переносом, тоF(M₁) =F(M₂). На рис. ниже изображены равные правильные треугольникиPQRи PQSи лучAB, перпендикулярный сторонеPQ. Легко видеть, чтоF(PQR) =aи F(PQS) = -a, где a — длина сторон этих правильных треугольников. Поэтому равные треугольникиPQRи PQSнельзя разрезать на части, переводящиеся друг в друга параллельным переносом.

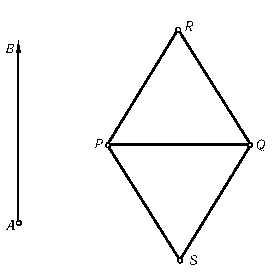
Ответ задачи отсутствует