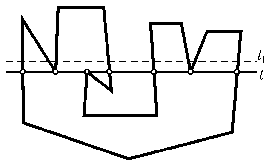
Прямая l задаёт две полуплоскости; одну из них будем называть верхней, а другую нижней. Пусть n₁ (соответственно n₂) – число вершин ломаной, лежащих на прямой l, для которых оба выходящих из них звена лежат в верхней (соответственно в нижней) полуплоскости, а m – число всех остальных точек пересечения прямой l и ломаной. Совершим обход ломаной, выйдя из некоторой точки, не лежащей на прямой l, и вернувшись в ту же точку. При этом мы переходим из одной полуплоскости в другую, только проходя через любую из m точек пересечения. Так как мы вернёмся в ту же точку, из которой начали обход, то m чётно. По условию  n₁ + n₂ + m = 1985,  поэтому число  n₁ + n₂  нечётно, то есть  n₁ ≠ n₂.  Пусть для определенности  n₁ > n₂.  Проведём тогда в верхней полуплоскости прямую l₁, параллельную l и удалённую от неё на расстояние меньшее чем любое ненулевое расстояние от l до вершин ломаной (см. рис.). Число точек пересечения ломаной с прямой l₁ равно  2n₁ + m > n₁ + n₂ + m = 1985,  то есть l₁ – искомая прямая.

Ответ задачи отсутствует