Задача
На отрезке длиной 1 расположены попарно не пересекающиеся отрезки, сумма длин которых равнаp. Обозначим эту систему отрезковA. ПустьB — дополнительная система отрезков (отрезки системAиBне имеют общих внутренних точек и полностью покрывают данный отрезок). Докажите, что существует параллельный переносT, для которого пересечениеBиT(A) состоит из отрезков, сумма длин которых не меньшеp(1 -p)/2.
Решение
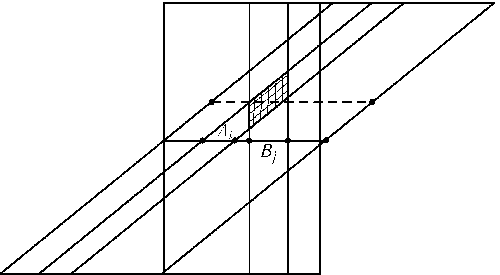
Пусть-1$\le$c$\le$1. Сдвинем данный отрезок наcвдоль себя, а затем сдвинем его наcв ортогональном направлении. Заштрихованная на рис. область соответствует пересечению отрезковAiиBj. Ее площадь равна произведению длин этих отрезков. Если рассмотреть все пары отрезков системAиB, то заштрихованная область будет иметь площадьp(1 -p). Поэтому некоторое горизонтальное сечение заштрихованных областей имеет длину не меньшеp(1 -p)/2.
Замечание. Если вместо отрезка рассматривать окружность (и вместо параллельного переноса поворот), тоp(1 -p)/2 можно заменить наp(1 -p).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь