Задача
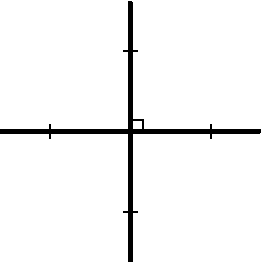
Назовем крестом фигуру, образованную диагоналями квадрата со стороной 1 (рис.). Докажите, что в круге радиуса 100 можно разместить лишь конечное число непересекающихся крестов.
Решение
Для каждого креста рассмотрим круг радиусом1/2$\sqrt{2}$с центром в центре креста. Докажем, что если пересекаются два таких круга, то пересекаются и сами кресты. Расстояние между центрами пересекающихся равных кругов не превосходит их удвоенного радиуса, поэтому расстояние между центрами соответствующих им крестов не превосходит 1/$\sqrt{2}$. Рассмотрим прямоугольник. заданный перекладинами первого креста и центром второго (рис.). Одна из перекладин второго креста проходит через этот прямоугольник, поэтому она пересекает первый крест, так как длина перекладины равна 1/$\sqrt{2}$, а длина диагонали прямоугольника не превосходит 1/$\sqrt{2}$. В круге конечного радиуса можно разместить лишь конечное число непересекающихся кругов радиуса1/2$\sqrt{2}$.
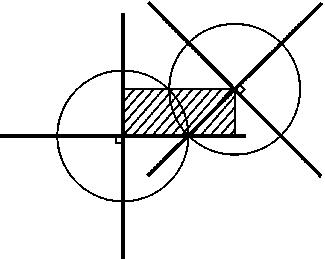
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь