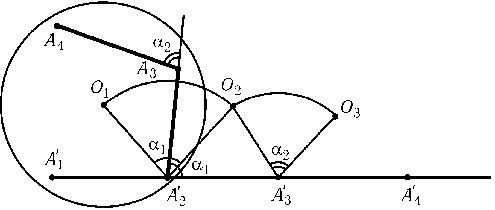
Предположим, что лев бежал по ломанойA₁A₂...A_n. Распрямим траекторию движения льва следующим образом. Повернем относительно точки A₂арену цирка и дальнейшую траекторию так, чтобы точка A₃попала на лучA₁A₂. Затем повернем относительно точки A₃арену цирка и дальнейшую траекторию так, чтобы точка A₄попала на лучA₁A₂и т. д. Центр Oарены цирка переходит при этом последовательно в точкиO₁=O,O₂,...,O_{n - 1}; точкиA₁,...,A_nпереходят в точкиA₁',...,A_n', лежащие на одной прямой (рис.). Пусть $\alpha_{i-1}^{}$ — угол поворота льва в точке A_i'. Тогда$\angle$O_{i - 1}A_i'O_i=$\alpha_{i-1}^{}$и A_i'O_{i - 1}=A_i'O_i$\le$10, поэтомуO_iO_{i - 1}$\le$10$\alpha_{i-1}^{}$. Следовательно,30 000 =A₁'A_n'$\le$A₁'O₁+O₁O₂+...+O_{n - 2}O_{n - 1}+O_{n - 1}A_n'$\le$10 + 10($\alpha_{1}^{}$+...+$\alpha_{n-2}^{}$) + 10, т. е.$\alpha_{1}^{}$+...+$\alpha_{n-2}^{}$$\ge$2998.

Ответ задачи отсутствует