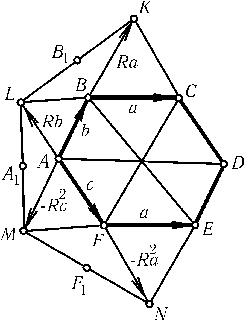
Пусть K,L,Mи N — вершины правильных треугольников, построенных на сторонахBC,AB,AFи FE;B₁,A₁и F₁ — середины отрезковKL,LMи MN(рис.). Пусть, далее,a=$\overrightarrow{BC}$=$\overrightarrow{FE}$,b=$\overrightarrow{AB}$и c=$\overrightarrow{AF}$;R — поворот на60^o, переводящий вектор$\overrightarrow{BC}$в $\overrightarrow{BK}$. Тогда$\overrightarrow{AM}$= -R²cи $\overrightarrow{FN}$= -R²a. Поэтому2$\overrightarrow{A_1B_1}$=R²c+Ra+bи 2$\overrightarrow{F_1A_1}$=R²a-c+Rb, т. е.$\overrightarrow{F_1A_1}$=R($\overrightarrow{A_1B_1}$).

Ответ задачи отсутствует