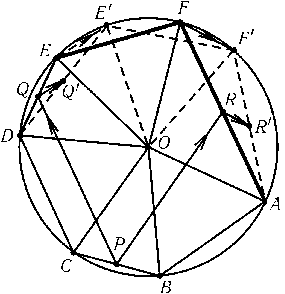
Пусть P,Qи R — середины сторонBC,DEи FA,O — центр описанной окружности. Предположим, что треугольникPQRправильный. Докажем, что тогда середины сторонBC,DE'и F'AшестиугольникаABCDE'F', в котором вершины E'и F'получены из точек Eи Fповоротом на некоторый угол относительно точки O, тоже образуют правильный треугольник. Этим будет все доказано, так как для правильного шестиугольника середины сторонBC,DEи FAобразуют правильный треугольник, а любой из рассматриваемых нами шестиугольников может быть получен из правильного поворотами треугольниковOCDи OEF. Пусть Q'и R' — середины сторонDE'и AF'(рис.). При повороте на60^oвекторпереходит в вектор. Так как=/2 и =/2, то векторпереходит в векторпри этом повороте. По предположению треугольникPQRправильный, т. е. вектор$\overrightarrow{PQ}$переходит в вектор$\overrightarrow{PR}$при повороте на60^o. Поэтому вектор=$\overrightarrow{PQ}$+переходит в вектор=$\overrightarrow{PR}$+при повороте на60^o, т. е. треугольникPQ'R'правильный.

Ответ задачи отсутствует