Задача
Даны точкаXи правильный треугольникABC. Докажите, что из отрезковXA,XBиXCможно составить треугольник, причем этот треугольник вырожденный тогда и только тогда, когда точкаXлежит на описанной окружности треугольникаABC(Помпею).
Решение
ПустьO — центр правильного треугольникаABC,x=$\overrightarrow{XO}$иa=$\overrightarrow{OA}$. Тогда$\overrightarrow{OB}$=R$\scriptstyle \alpha$aи$\overrightarrow{OC}$=R2$\scriptstyle \alpha$a, где$\alpha$= 120o. Поэтому
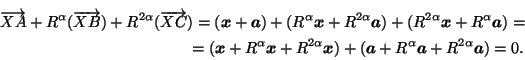
Это означает, что векторы$\overrightarrow{XA}$,R$\scriptstyle \alpha$($\overrightarrow{XB}$) иR2$\scriptstyle \alpha$($\overrightarrow{XC}$) являются векторами сторон некоторого треугольника. Вырожденность треугольника эквивалентна сонаправленности двух их этих векторов. Если, например, векторы$\overrightarrow{XA}$иR$\scriptstyle \alpha$($\overrightarrow{XB}$), то$\angle$(AX,XB) =$\angle$(AC,CB), поэтому точкаXлежит на описанной окружности треугольникаABC. Вырожденность треугольника в том случае, когда точкаXлежит на описанной окружности, доказана в задаче 18.13.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет