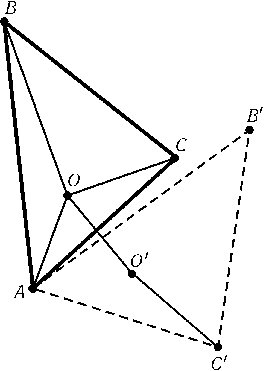
а) Пусть O — произвольная точка. При повороте на60^oотносительно точки Aточки B,Cи Oпереходят в некоторые точки B',C'и O'(рис.). Так какAO=OO'и OC=O'C', тоBO+AO+CO=BO+OO'+O'C'. Длина ломанойBOO'C'минимальна тогда, когда эта ломаная является отрезком, т. е.$\angle$AOB=$\angle$AO'C'=$\angle$AOC= 120^o. Для построения искомой точки можно воспользоваться результатом задачи 2.8. Требуемая точка внутри треугольникаABCсуществует тогда и только тогда, когда все его углы меньше120^o. Если один из углов равен120^o, то требуемая точка — вершина этого угла. Замечание. По поводу случая, когда у треугольника есть угол больше120^o, см. задачу 18.29B. б) Сумма расстояний от точки Oдо вершин равна длине отрезкаBC', полученного при решении задачи а). Ясно также, что(BC')²=b²+c²- 2bccos($\alpha$+ 60^o) =b²+c²-bccos$\alpha$+bc$\sqrt{3}$sin$\alpha$= (a²+b²+c²)/2 + 2$\sqrt{3}$S.

Ответ задачи отсутствует