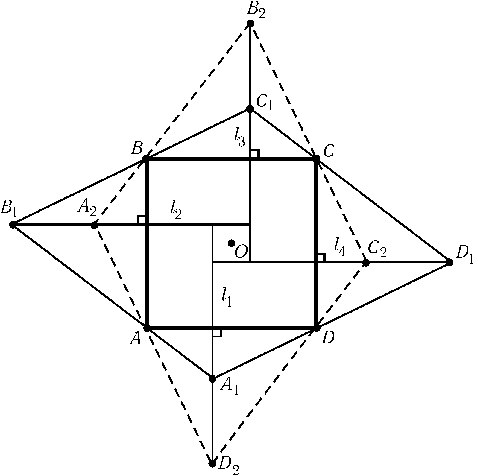
Вокруг квадратаABCDописан параллелограммA₁B₁C₁D₁(точка Aлежит на сторонеA₁B₁,B — наB₁C₁и т. д.). Опустим из вершин A₁,B₁,C₁и D₁перпендикуляры l₁,l₂,l₃и l₄на стороны квадрата. Чтобы доказать, что эти прямые образуют квадрат, достаточно проверить, что при повороте на90^oотносительно центра OквадратаABCDпрямые l₁,l₂,l₃и l₄переходят друг в друга. При повороте относительно точки Oна90^oточки A₁,B₁,C₁и D₁переходят в точки A₂,B₂,C₂и D₂(рис.).

Так какAA₂$\perp$B₁Bи BA₂$\perp$B₁A, тоB₁A₂$\perp$AB. Это означает, что прямая l₁переходит при повороте на90^oотносительно точки Oв прямую l₂. Для остальных прямых доказательство аналогично.

Ответ задачи отсутствует