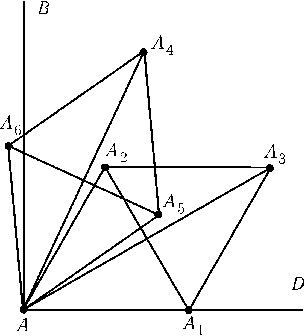
а) Фигуру, лежащую внутри квадратаABCDсо стороной 1, обозначим через F, а ее площадь — через S. Рассмотрим два вектора$\overrightarrow{AA_1}$и $\overrightarrow{AA_2}$, где точка A₁лежит на сторонеADи AA₁= 0, 001, а точка A₂лежит внутри углаBAD,$\angle$A₂AA₁= 60^oи AA₂= 0, 001 (рис.). Пусть F₁и F₂ — образы Fпри параллельных переносах на векторы$\overrightarrow{AA_1}$и $\overrightarrow{AA_2}$. Фигуры F,F₁и F₂не имеют общих точек и лежат внутри квадрата со стороной 1, 001. Поэтому3S< 1, 001², т. е.S< 0, 335 < 0, 34. б) Рассмотрим вектор$\overrightarrow{AA_3}$=$\overrightarrow{AA_1}$+$\overrightarrow{AA_2}$. Повернем вектор$\overrightarrow{AA_3}$вокруг точки A(против часовой стрелки на острый угол) так, чтобы точка A₃перешла в точку A₄, для которойA₃A₄= 0, 001. Рассмотрим также векторы$\overrightarrow{AA_5}$и $\overrightarrow{AA_6}$длиной 0, 001, образующие с вектором$\overrightarrow{AA_4}$углы 30^oи лежащие по разные стороны от него (рис.). Обозначим образ фигуры Fпри параллельном переносе на вектор$\overrightarrow{AA_i}$через F_i. Для определенности будем считать, чтоS(F₄$\cap$F)$\le$S(F₃$\cap$F). ТогдаS(F₄$\cap$F)$\le$S/2, поэтомуS(F₄$\cup$F)$\ge$3S/2. Фигуры F₅и F₆не пересекаются ни друг с другом, ни с фигурами Fи F₄, поэтомуS(F$\cup$F₄$\cup$F₅$\cup$F₆)$\ge$7S/2. (Если бы оказалось, чтоS(F₃$\cap$F)$\le$S(F₄$\cap$F), то вместо фигур F₅и F₆нужно было бы взять F₁и F₂.) Так как длины векторов$\overrightarrow{AA_i}$не превосходят 0, 001$\sqrt{3}$, все рассматриваемые фигуры лежат внутри квадрата со стороной 1 + 0, 002$\sqrt{3}$. Поэтому7S/2$\le$(1 + 0, 002$\sqrt{3}$)²и S< 0, 287. римечаниеS(A$\cup$B) — площадь объединения фигур Aи B,S(A$\cap$B) — площадь их пересечения.

Ответ задачи отсутствует