Задача
Внутри каждой стороны параллелограмма выбрано по точке. Выбранные точки сторон, имеющих общую вершину, соединены. Докажите, что центры описанных окружностей четырех получившихся треугольников являются вершинами некоторого параллелограмма.
Решение
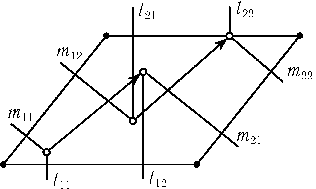
Обозначим серединные перпендикуляры к сторонам треугольников так, как показано на рис. Все прямыеlijпараллельны и расстояние между прямымиl11иl12равно расстоянию между прямымиl21иl22(оно равно половине длины стороны параллелограмма). Поэтому параллельный перенос, переводящийl11вl12, переводитl21вl22, а параллельный перенос, переводящийl11вl21, переводитl12вl22. Следовательно, параллельный перенос, переводящий точку пересечения прямыхl11иm11в точку пересечения прямыхl12иm21, переводит точку пересечения прямыхl21иm12в точку пересечения прямыхl22иm22.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь