Задача
Через центр O правильного треугольника ABC проведена прямая, пересекающая прямые BC, CA и AB в точках A1, B1 и C1.
Докажите, что одно из чисел 1/OA1, 1/OB1 и 1/OC1 равно сумме двух других.
Решение
Рассмотрим случай, когда точка C1 лежит на продолжении стороны AB за точку A, и докажем, что 1/OA1 = 1/OB1 + 1/OC1. Опустим перпендикулярыB1D, OEиA1FнаAB, B1KнаOEиOLнаA1F. Пусть OK = x, OE = r, A1L = y, тогда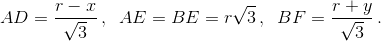 
ТреугольникиA1OL, OB1KиOC1Eподобны, поэтому достаточно доказать, что
1/A1L=1/OK+1/OE, то есть что 1/y=1/x+1/r.
Из подобия тех же треугольников OL/A1L=BK/OK, то есть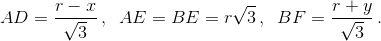 
что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет