Задачи и олимпиады по математике

Задача

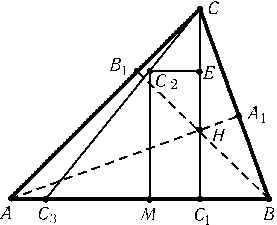
В треугольнике ABCпроведены высоты AA₁,BB₁и CC₁. Пусть A₁A₂,B₁B₂и C₁C₂ — диаметры окружности девяти точек треугольника ABC. Докажите, что прямые AA₂,BB₂и CC₂пересекаются в одной точке (или параллельны).

Решение

Пусть H — точка пересечения высот треугольника ABC, Eи M — середины отрезков CHи AB(рис.). Тогда C₁MC₂E — прямоугольник. Пусть прямая CC₂пересекает прямую ABв точке C₃. Докажем, что $\overline{AC_3}$:$\overline{C_3B}$=tg2$\beta$:tg2$\alpha$. Легко проверить, что $\overline{C_3M}$:$\overline{C_2E}$=$\overline{MC_2}$:$\overline{EC}$,$\overline{EC}$=Rcos$\gamma$,$\overline{MC_2}$=$\overline{C_1E}$= 2Rsin$\alpha$sin$\beta$-Rcos$\gamma$и $\overline{C_2E}$=$\overline{MC_1}$=Rsin($\beta$-$\alpha$), поэтому

$\displaystyle \overline{C_3M}$ = R sin($\displaystyle \beta$ - $\displaystyle \alpha$)(2 sin$\displaystyle \beta$sin$\displaystyle \alpha$ - cos$\displaystyle \gamma$)/cos$\displaystyle \gamma$ = R sin($\displaystyle \beta$ - $\displaystyle \alpha$)cos($\displaystyle \beta$ - $\displaystyle \alpha$)/cos$\displaystyle \gamma$.

Следовательно,

$\displaystyle {\frac{\overline{AC_3}}{\overline{C_3B}}}$ = $\displaystyle {\frac{\overline{AM}+\overline{MC_3}}{\overline{C_3M}+\overline{MB}}}$ = $\displaystyle {\frac{\sin2\gamma +\sin2(\alpha -\beta )}{\sin2\gamma -\sin2(\alpha -\beta )}}$ = $\displaystyle {\frac{{\rm tg}2\beta }{{\rm tg}2\alpha }}$.

Аналогичные рассуждения показывают, что

$\displaystyle {\frac{\overline{AC_3}}{\overline{C_3B}}}$^.$\displaystyle {\frac{\overline{BA_3}}{\overline{A_3C}}}$^.$\displaystyle {\frac{\overline{CB_3}}{\overline{B_3A}}}$ = $\displaystyle {\frac{{\rm tg}2\beta }{{\rm tg}2\alpha }}$^.$\displaystyle {\frac{{\rm tg}2\gamma }{{\rm tg}2\beta }}$^.$\displaystyle {\frac{{\rm tg}2\alpha }{{\rm tg}2\gamma }}$ = 1.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления