Задача
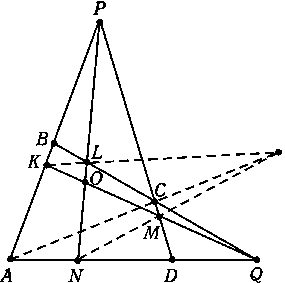
а) Через точки Pи Qпроведены тройки прямых. Обозначим их точки пересечения так, как показано на рис. Докажите, что прямые KL,ACи MNпересекаются в одной точке (или параллельны). б) Докажите, далее, что если точка Oлежит на прямой BD, то точка пересечения прямых KL,ACи MNлежит на прямой PQ.
Решение
а) Пусть R — точка пересечения прямых KLи MN. Применяя теорему Паппа к тройкам точек (P,L,N) и (Q,M,K), получаем, что точки A,Cи Rлежат на одной прямой. б) Применяя теорему Дезарга к треугольникам NDMи LBK, получаем, что точки пересечения прямых NDи LB, DMи BK, NMи LKлежат на одной прямой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет