Задача
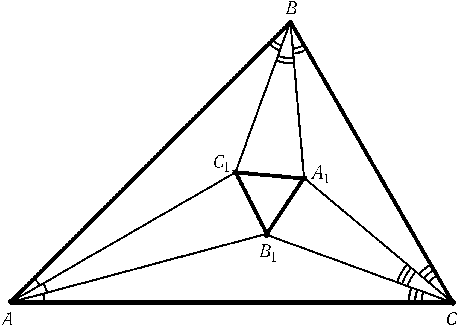
В треугольникеABCпроведены триссектрисы (лучи, делящие углы на три равные части). Ближайшие к сторонеBCтриссектрисы угловBиCпересекаются в точкеA1; аналогично определим точкиB1иC1(см. рис.). Докажите, что треугольник A1B1C1равносторонний.
Решение
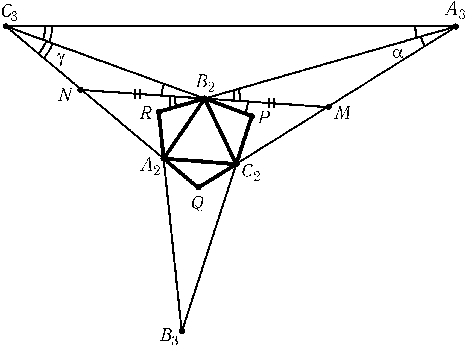
Пусть в исходном треугольнике ∠A = 3α, ∠B = 3β и ∠C = 3γ. Возьмём равносторонний треугольник A2B2C2 и построим на его сторонах как на основаниях равнобедренные треугольники A2B2R, B2C2P и C2A2Q с углами при основаниях 60° – γ, 60° – α, 60° – β соответственно (см. рис.). Продолжим боковые стороны этих треугольников за точки A2, B2 и C2 и обозначим точку пересечения продолжений сторон RB2 и QC2 через A3, PC2 и RA2 – через B3, QA2 и PB2 – через C3. Проведём через B2 прямую, параллельную A2C2, и обозначим через M и N точки её пересечения с прямыми QA3 и QC3. Ясно, что B2 – середина отрезка NM.
Вычислим углы треугольников B2C3N и B2A3M: ∠C3B2N = ∠PB2M = ∠C2B2M – ∠C2B2P = α, ∠B2NC3 = 180° – ∠C2A2Q = 120° + β, значит,
∠B2C3N = 180° – α – (120° + β) = γ. Аналогично ∠A3B2M = γ и ∠B2A3M = α.
Следовательно, треугольники B2C3N и A3B2M подобны. Значит, C3B2 : B2A3 = C3N : B2M, а так как B2M = B2N и ∠C3B2A3 = ∠C3NB2, то
C3B2 : B2A3 = C3N : NB2 и треугольники C3B2A3 и C3NB2 подобны, следовательно, ∠B2C3A3 = γ. Аналогично ∠A2C3B3 = γ, а значит,
∠A3C3B3 = 3γ = ∠C и C3B2, C3A2 – триссектрисы угла C3 треугольника A3B3C3. Аналогичные рассуждения для вершин A3 и B3 показывают, что треугольники ABC и A3B3C3 подобны, а точки пересечения триссектрис треугольника A3B3C3 образуют правильный треугольник A2B2C2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь