Задача
На сторонах треугольника ABC взяты точки A1, B1 и C1 так, что AB1 : B1C = cn : an, BC1 : C1A = an : bn и CA1 : A1B = bn : cn (a, b, c – длины сторон треугольника). Описанная окружность треугольника A1B1C1 высекает на сторонах треугольника ABC отрезки длиной ±x, ±y и ±z (знаки выбираются в соответствии с ориентацией треугольника). Докажите, что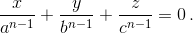 
Решение
Пусть a1 = BA1, a2 = A1C, b1 = CB1, b2 = B1A, c1 = AC1 и c2 = C1B. Произведения длин отрезков секущих, проходящих через одну точку, равны, поэтому
a1(a1 + x) = c2(c2 - z), то есть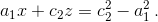 
Аналогично, 
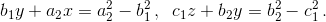Домножим первое уравнение на b2n, второе – на с2n, третье – на a2n и сложим. Так как, например, c2bn – c1an = 0 по условию, то в правой части получим нуль. В левой части коэффициент при x равен 
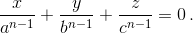Поэтому abncnx + bancny + canbnz = 0. Поделив обе части равенства
на (abc)n, получим требуемое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь