Задача
В каждый из углов треугольника ABC вписано по окружности. Из одной вершины окружности, вписанные в два других угла, видны под равными углами. Из другой – тоже. Докажите, что тогда и из третьей вершины две окружности видны под равными углами.
Решение
Пусть из вершины A окружности, вписанные в углы B и C, видны под углами αb и αc, а радиусы этих окружностей равны rb и rc. Тогда
b = rc(ctg γ/2 + ctg αc/2) и c = rb(ctg β/2 + ctg αb/2).
Поэтому равенство αb и αc эквивалентно равенству b/rc – ctg γ/2 = c/rb – ctg β/2, то есть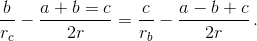 
После несложных преобразований получаем равенство 
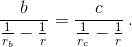Ясно, что из этого равенства и из равенства 
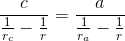следует равенство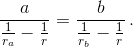 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет