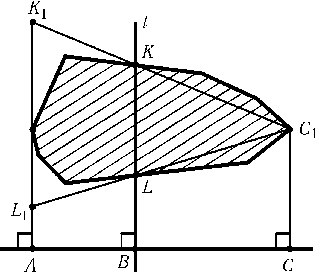
Обозначим проекцию прямой l через B, крайние точки проекции многоугольника – через A и C. Пусть C₁ – точка многоугольника, проецирующаяся в точку C; прямая l пересекает многоугольник в точках K и L, а K₁ и L₁ – точки прямых C₁K и C₁L, проецирующиеся в точку A (см. рисунок).

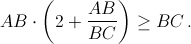   Одна из частей, на которые прямая l делит многоугольник, содержится в трапеции K₁KLL₁, другая содержит треугольник C₁KL. Поэтому  S_K1KLL1 ≥ S_C1KL,  то есть  AB·(KL + K₁L₁) ≥ BC·KL.  Так как  K₁L₁ : KL = (AB + BC) : BC,  то     Решая это квадратное неравенство, получаем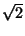  

   Аналогично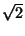  

Ответ задачи отсутствует