Задача
Каждая из трех прямых делит площадь фигуры пополам. Докажите, что часть фигуры, заключенная внутри треугольника, образованного этими прямыми, имеет площадь, не превосходящую 1/4 площади всей фигуры.
Решение
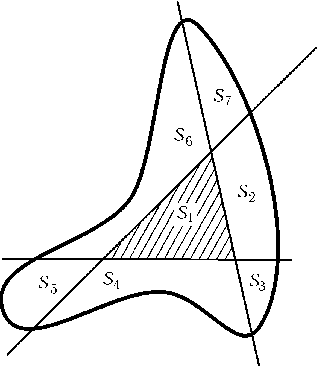
Обозначим площади частей фигуры, на которые ее делят прямые, так, как показано на рис. Площадь всей фигуры обозначим через S. Так как S3+ (S2+S7) =S/2 =S1+S6+ (S2+S7), то S3=S1+S6. Складывая это равенство с равенством S/2 =S1+S2+S3+S4, получаем S/2 = 2S1+S2+S4+S6$\geq$2S1, т. е. S1$\leq$S/4.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет