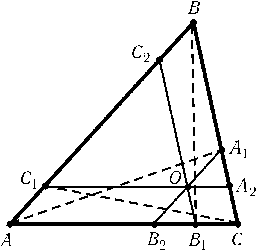
Через точку O, лежащую внутри треугольника ABC, проведены отрезки, параллельные сторонам. Отрезки AA₁,BB₁и CC₁разбивают треугольник ABCна четыре треугольника и три четырехугольника (рис.). Докажите, что сумма площадей треугольников, прилегающих к вершинам A,Bи C, равна площади четвертого треугольника.