Задача
В треугольнике ABCточка E — середина стороны BC, точка Dлежит на стороне AC,AC= 1,$\angle$BAC= 60o,$\angle$ABC= 100o,$\angle$ACB= 20oи $\angle$DEC= 80o(рис.). Чему равна сумма площади треугольника ABCи удвоенной площади треугольника CDE?
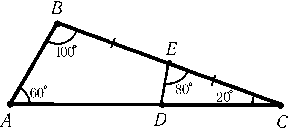
Решение
Опустим из точки Cперпендикуляр lна прямую AB. Пусть точки A',B'и E'симметричны точкам A,Bи Eотносительно прямой l. Тогда треугольник AA'Cравносторонний, причем $\angle$ACB=$\angle$BCB'=$\angle$B'CA'= 20o. Треугольники EE'Cи DECравнобедренные с углом при вершине 20o, причем боковая сторона ECу них общая. Следовательно, SABC+ 2SEDC=SABC+ 2SEE'C. Так как Eсередина BC, то 2SEE'C=SBE'C=SBB'C/2. Поэтому SABC+ 2SEDC=SAA'C/2 =$\sqrt{3}$/8.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь