Задача
Внутри данного треугольника ABCнайдите такую точку O, что площади треугольников BOL,COMи AONравны (точки L,Mи Nлежат на сторонах AB,BCи CA, причем OL||BC,OM||ACи ON||AB; рис.).
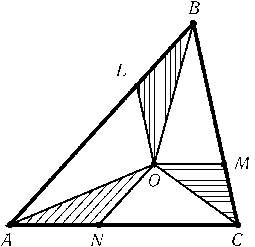
Решение
Обозначим точку пересечения прямой LOсо стороной ACчерез L1. Так как SLOB=SMOCи $\triangle$MOC=$\triangle$L1OC, то SLOB=SL1OC. Высоты треугольников LOBи L1OCравны, поэтому LO=L1O, т. е. точка Oлежит на медиане, проведенной из вершины A. Аналогично доказывается, что точка Oлежит на медианах, проведенных из вершин Bи C, т. е. O — точка пересечения медиан треугольника. Проведенные рассуждения показывают также, что точка пересечения медиан треугольника обладает требуемым свойством.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет