а) Пусть X — точка пересечения описанных окружностей треугольников ABCи AB'C'. Тогда $\angle$(XB',XC) =$\angle$(XB',XA) +$\angle$(XA,XC) =$\angle$(C'B',C'A) +$\angle$(BA,BC). Так как AC'=AP=AB', то треугольник C'AB'равнобедренный, причем $\angle$C'AB'= 2$\angle$A, поэтому $\angle$(C'B',C'A) =$\angle$A- 90^o. Следовательно, $\angle$(XB',XC) =$\angle$A- 90^o+$\angle$B= 90^o-$\angle$C=$\angle$(A'B',A'C), т. е. точка Xлежит на описанной окружности треугольника A'B'C. Для описанной окружности треугольника A'BC'доказательство аналогично. б) Пусть X — точка пересечения описанных окружностей треугольников A'B'C'и A'BC. Докажем, что она лежит на описанной окружности треугольника ABC'. Ясно, что $\angle$(XB,XC') =$\angle$(XB,XA') +$\angle$(XA',XC') =$\angle$(CB,CA') +$\angle$(B'A',B'C'). Пусть A₁,B₁и C₁ — середины отрезков PA',PB'и PC'. Тогда $\angle$(CB,CA') =$\angle$(CP,CA₁) =$\angle$(B₁P,B₁A₁),$\angle$(B'A',B'C') =$\angle$(B₁A₁,B₁C₁) и $\angle$(AB,AC') =$\angle$(AP,AC₁) =$\angle$(B₁P,B₁C₁). Следовательно, $\angle$(XB,XC') =$\angle$(AB,AC'). Аналогично доказывается, что точка Xлежит на описанной окружности треугольника AB'C. в) Так как QA' — общая хорда окружностей с центрами Oи I, то QA'$\perp$OI. Аналогично QB'$\perp$OJи QC$\perp$IJ. Поэтому стороны углов OJIи B'QC, а также углов OIJи A'QCвзаимно перпендикулярны, а значит, sin OJI= sin B'QCи sin OIJ= sin A'QC. Следовательно, OI:OJ= sin OJI: sin OIJ= sin B'QC:A'QC. Ясно также, что

$\displaystyle {\frac{QI}{QJ}}$ = $\displaystyle {\frac{\sin QJI}{\sin QIJ}}$ = $\displaystyle {\frac{\sin(QJC/2)}{\sin(QIC/2)}}$ = .

$\displaystyle {\frac{OI}{OJ}}$ : $\displaystyle {\frac{QI}{QJ}}$ = : = 1.

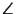Ответ задачи отсутствует