Задача
ABCD- вписанный четырехугольник, диагонали которого перпендикулярны.P- точка пересечения диагоналей. Докажите, что прямая, проведенная из точки Pперпендикулярно BC, делит сторону ADпополам.
Решение
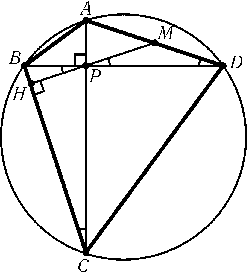
Пусть перпендикуляр, опущенный из точки Pна BC, пересекает BCв точке Hи ADв точке M(рис.).$\angle$BDA=$\angle$BCA=$\angle$BPH=$\angle$MPD. Из равенства углов MDPи MPDследует, что MP — медиана прямоугольного треугольника APD. В самом деле,$\angle$APM= 90o-$\angle$MPD= 90o-$\angle$MDP=$\angle$PAM, т. е. AM=PM=MD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет