Задача
В каком месте следует построить мост MN через реку, разделяющую две данные деревни A и B, чтобы путь AMNB из деревни A в деревню B был кратчайшим (берега реки считаются параллельными прямыми, мост предполагается перпендикулярным к реке).
Решение
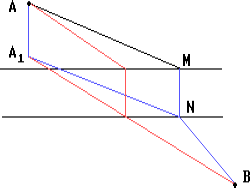
Предположим, что некоторое положение моста найдено. При параллельном переносе на вектор $\overrightarrow{MN}$ точка A перейдёт в некоторую точку A1, а точка M — в точку N. Тогда
AM + MN + NB = AA1 + A1N + NB $\displaystyle \geqslant$ AA1 + A1B
(неравенство треугольника), причём равенство достигается,
если точкиA1,NиBлежат на одной прямой, т.е.BN||AM.
Отсюда вытекает следующий способ построения.
Отложим от точки A отрезок AA1, по величине равный ширине
реки и перпендикулярный к её направлению, соединим точку A1 с
точкой B. Точка N, полученная при пересечении A1B с более близким
к B берегом реки, определит положение моста.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет