Задача
Из вершины C прямого угла прямоугольного треугольника ABC проведена высота CD, и в треугольники ACD и BCD вписаны окружности с центрами P и Q. Общая внешняя касательная к этим окружностям пересекает катеты AC и BC в точках M и N, а высоту CD — в точке K. Докажите, что:
а) треугольники CMN и CBA подобны;
б) точки C, M, N, P и Q лежат на окружности с центром K, радиус которой равен радиусу вписанной окружности треугольника ABC.
Решение
Поскольку KP и KQ — биссектрисы смежных углов, то $\angle$PKQ = 90o. Аналогично $\angle$PDQ = 90o. Поэтому точки K и D лежат на окружности с диаметром PQ. Следовательно,
$\displaystyle \angle$KPQ = $\displaystyle \angle$KDQ = 45o.
ПоэтомуPKQ— равнобедренный прямоугольный треугольник.
Докажем теперь, что прямоугольный треугольник PDQ подобен
треугольнику ACB. Действительно, треугольник ADC подобен
треугольнику CDB по двум углам, а т.к. коэффициент подобия равен
отношению
${\frac{r_{1}}{r_{2}}}$ радиусов вписанных окружностей этих
треугольников, то
$\displaystyle {\frac{DP}{DQ}}$ = $\displaystyle {\frac{r_{1}\sqrt{2}}{r_{2}\sqrt{2}}}$ = $\displaystyle {\frac{r_{1}}{r_{2}}}$ = $\displaystyle {\frac{AC}{BC}}$.
Следовательно, треугольникиPDQиACBподобны. Тогда
$\displaystyle \angle$QKD = $\displaystyle \angle$DPQ = $\displaystyle \angle$CAD = $\displaystyle \angle$BCD,
поэтомуKQ||CB. АналогичноKP||CA. Следовательно,
$\displaystyle \angle$CMN = $\displaystyle \angle$MKP = $\displaystyle \angle$DKP = $\displaystyle \angle$PQD = $\displaystyle \angle$CBA.
Значит, треугольникCMNподобен треугольникуCBA.
Поскольку
$\angle$CMK = $\angle$ABC = $\angle$ACD, то треугольник MKC —
равнобедренный, поэтому KC = KM. Аналогично KC = KN.
Поскольку KQ || CN, а CQ — биссектриса угла KCN,
$\displaystyle \angle$CQK = $\displaystyle \angle$QCN = $\displaystyle \angle$QCK.
Поэтому треугольникCKQ— равнобедренный иKQ=KC. АналогичноKP=KC. Следовательно, точкиC,M,N,PиQлежат на окружности с
центромK. Вычислим радиус этой окружности.
Пусть r — радиус вписанной окружности треугольника ABC. Тогда
r2 = r21 + r22, PQ2 = PD2 + QD2 = 2r21 + 2r22 = 2r2.
Следовательно,KQ=${\frac{PQ}{\sqrt{2}}}$=r.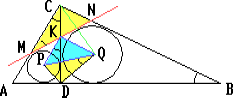
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет