Задача
Равносторонние треугольники ABC и PQR расположены так, что вершина C лежит на стороне PQ, а вершина R — на стороне AB. Докажите, что AP || BQ.
Решение
Отрезок CR виден из точек B и Q под углом 60o, поэтому точки C, Q, B, R лежат на одной окружности. Аналогично точки C, P, A, R также лежат на одной окружности. Поэтому
$\displaystyle \angle$APQ = $\displaystyle \angle$APC = 180o - $\displaystyle \angle$ARC = $\displaystyle \angle$CRB = 180o - $\displaystyle \angle$CQB = $\displaystyle \angle$PQB.
Следовательно,AP||BQ.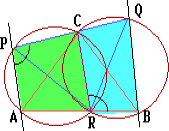
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет