Задача
Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие — на хорде. Чему равна разность длин сторон квадратов?
Решение
Пусть O — центр окружности, PQ — указанная хорда, H — её середина (OH = h), ABCD и KLMN — указанные квадраты (рис.1), E и F — середины отрезков MN и BC. Обозначим стороны этих квадратов через a и b соответственно, а радиус окружности — через r.
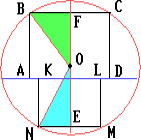
Из прямоугольниых треугольников OEN и OFB находим, что
b + h = HE + OH = EO = $\displaystyle \sqrt{ON^{2} - NE^{2}}$ = $\displaystyle \sqrt{r^{2} - \frac{b^{2}}{4}}$,
a - h = HF - OH = FO = $\displaystyle \sqrt{OB^{2} - FB^{2}}$ = $\displaystyle \sqrt{r^{2} - \frac{a^{2}}{4}}$.
Поэтому
(b + h)2 = r2 - $\displaystyle {\frac{b^{2}}{4}}$, (a - h)2 = r2 - $\displaystyle {\frac{a^{2}}{4}}$.
Вычитая почленно эти равенства, получим, что
(b + h)2 - (a - h)2 = $\displaystyle {\frac{a^{2} - b^{2}}{4}}$, 2h - (a - b) = $\displaystyle {\frac{a - b}{4}}$.
Отсюда находим, чтоa-b=${\frac{8}{5}}$h.
Ответ
${\frac{8}{5}}$h.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет