Задача
Известно, что AE и CD — биссектрисы треугольника ABC,
$\angle$CDE = 30o. Докажите, что один из углов треугольника ABC равен 60o или 120o.
Решение
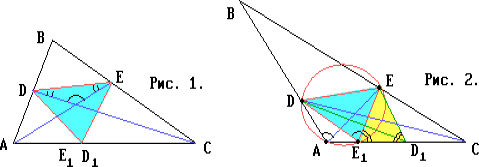
Обозначим через O точку пересечения биссектрис треугольника ABC. Пусть D1 — образ точки D при симметрии относительно прямой AE, E1 — образ точки E при симметрии относительно прямой CD. Тогда точки D1 и E1 лежат на прямой AC.
Треугольник DEE1 — равносторонний, т.к. DE = DE1, а
$\angle$EDE1 = 2$\angle$EDC = 60o.
Если точки E1 и D1 совпадают (рис.1), то EA — биссектриса угла DEE1. Поэтому
$\displaystyle \angle$DEA = 30o, $\displaystyle \angle$DOE = 120o,
а т.к.$\angle$DOE= 90o+${\frac{1}{2}}$$\angle$B, то$\angle$B= 60o.
Пусть теперь точки E1 и D1 различны (рис.2). Поскольку
ED1 = ED = EE1, то треугольник
D1EE1 — равнобедренный.
Поэтому
$\displaystyle \angle$ADE = $\displaystyle \angle$AD1E = $\displaystyle \angle$EE1C = 180o - $\displaystyle \angle$AE1E.
Следовательно, точкиA,D,EиE1лежат на одной окружности.
Поэтому
$\displaystyle \angle$DAE = $\displaystyle \angle$DE1E = 60o, $\displaystyle \angle$BAC = 120o.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет